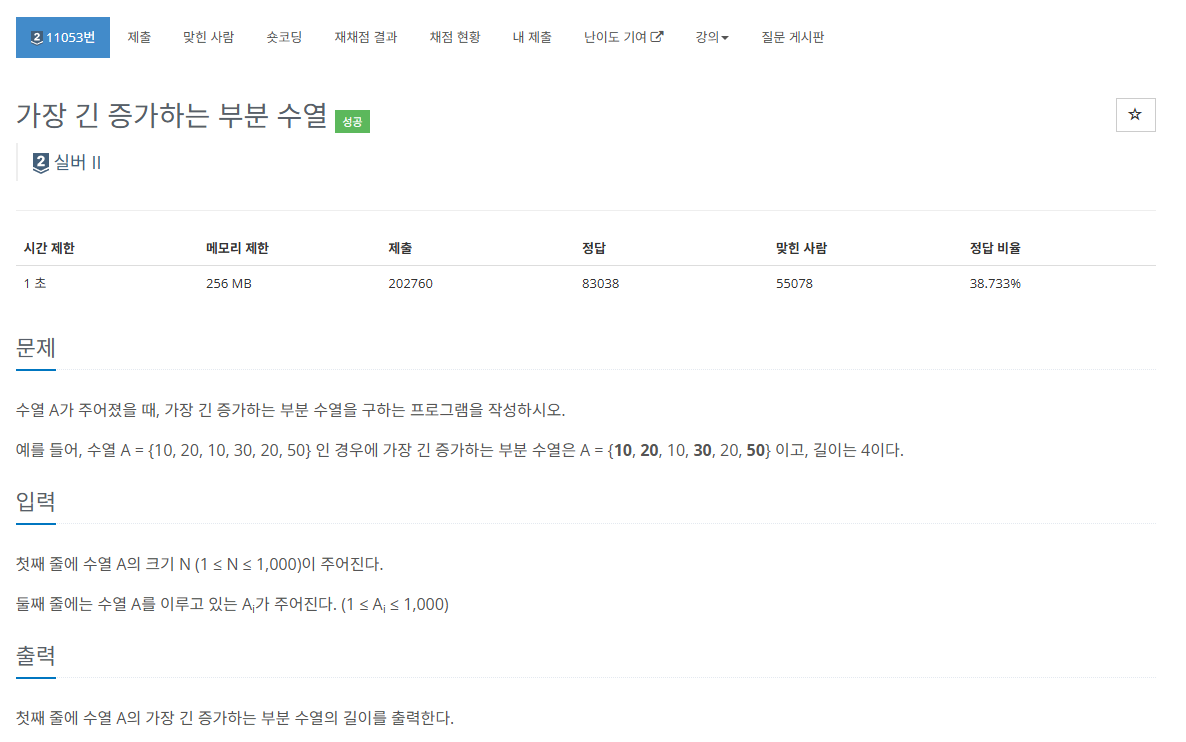
문제 설명
- 첫째 줄에 수열 크기 A 입력
- 둘째 줄에 수열 입력
- 수열에서의 증가하는 부분이 가장 긴 부분의 길이를 출력
문제 풀이
처음에는 DP라서 점화식을 구해서 재귀로 푸는 문제로 이해했다.
따라서 최대값과 그 이전의 값(최대값보다 작은 최대값)을 저장해서 인접 행렬을 순차적으로 탐색하였다.
이 방법은 자기보다 작은 수를 만났을 때 초기화해서 다시 탐색해서 비교해야 하는 부분에서 잘못된 방법이라는 것을 느꼈다.
AI한테 도움을 받아 접근 방식에 대한 아이디어를 받은 부분은 다음과 같이 접근하였다.
수열을 제일 작은 수열에서부터 하나씩 크기를 키워 증가하는 부분이 가장 길 때의 길이를 비교하는 방식이다.
예를 들면 아래와 같다.
예시 입력값
6
10 20 10 30 20 50위와 같이 입력을 받은 경우
A1 = [10]
A2 = [10, 20]
A3 = [10, 20, 10]
A4 = [10, 20, 10, 30]
A5 = [10, 20, 10, 30, 20]
A6 = [10, 20, 10, 30, 20, 50]
이런식으로 쪼개서 계산을 하는 것이다.
A1의 경우 증가하는 부분이 가장 긴 길이가 1일 것이고
A2의 경우 길이가 A1 길이 + 1, A1 길이 중 최대값일 것이고
A3의 경우 10은 이전 원소들이 작은 값이 없기 때문에 길이가 1,
A4의 경우 30이 이전 원소들보다 크기 때문에 이전(A1~ A3) 길이들 중 최대값 +1의 길이일 것이고
...
A6의 경우 A4와 마찬가지로 50이 이전 원소들보다 크기 때문에 A1~A5 길이 중 최대값의 + 1일 것이다.
따라서 점화식은 다음과 같다.
Ai의 길이 = Max(현재 수가 이전 원소보다 클 경우 해당 원소의 길이 + 1, 현재 수가 이전 원소보다 작을 경우 이전 원소의 길이들 중 최대값)
이걸 코드로 구현하면 아래와 같다
코드 풀이
using System;
using System.Collections.Generic;
using System.Linq;
namespace StudyCS
{
class Program
{
public static void Main(string[] args)
{
//입력처리
int length = int.Parse(Console.ReadLine());
int[] sequence = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
Solve(sequence);
}
public static void Solve(int[] inSequence)
{
int[] maxLength = Enumerable.Repeat(1,inSequence.Length).ToArray();
Search(inSequence, ref maxLength);
Console.WriteLine(maxLength.Max());
}
public static void Search(int[] inSequence, ref int[] maxLength)
{
//자기가 최대값일 때 원소 앞에 있는 원소 중 차례로 자기보다 작은 값 찾기
for (int i = 1; i < inSequence.Length; i++)
{
for(int j = 0; j < i; j++)
{
if(inSequence[j] < inSequence[i])
{
maxLength[i] = Math.Max(maxLength[i], maxLength[j] + 1);
}
}
}
}
}
}- 이중 반복문을 통해 자신의 Index 전까지 탐색을 반복
- 현재 추가된 최대값인 수(inSequence[i])보다 탐색하는 수(inSequence[j])가 작은지 판별한다.
- 만약 작다면 그 수를 최대값으로 한 수열의 길이 +1 혹은 지금 저장된 이전 수열들의 길이 중 최대값을 저장한다.
알고리즘을 워낙 등한시했어서 dp 알고리즘 역시 익숙해지려면 시간이 좀 필요할 것 같다. 다음에도 dp 문제를 풀어야할 것 같다.
'BaekJoon' 카테고리의 다른 글
| Greedy - 15748 (0) | 2025.09.16 |
|---|---|
| Dynamic Programming - 11060 (0) | 2025.09.12 |
| BFS - 18352 (0) | 2025.09.10 |
| 백트래킹 - 4251 (0) | 2025.09.09 |
| 그래프와 순회 - 24479 (0) | 2025.03.30 |