백준 온라인 코딩 문제풀이
Baekjoon Online Judge
Baekjoon Online Judge 프로그래밍 문제를 풀고 온라인으로 채점받을 수 있는 곳입니다.
www.acmicpc.net
단계별로 풀어보기 - 그래프와 순회 단계 - 24479번 알고리즘 수업 - 깊이 우선 탐색 1 문제이다.
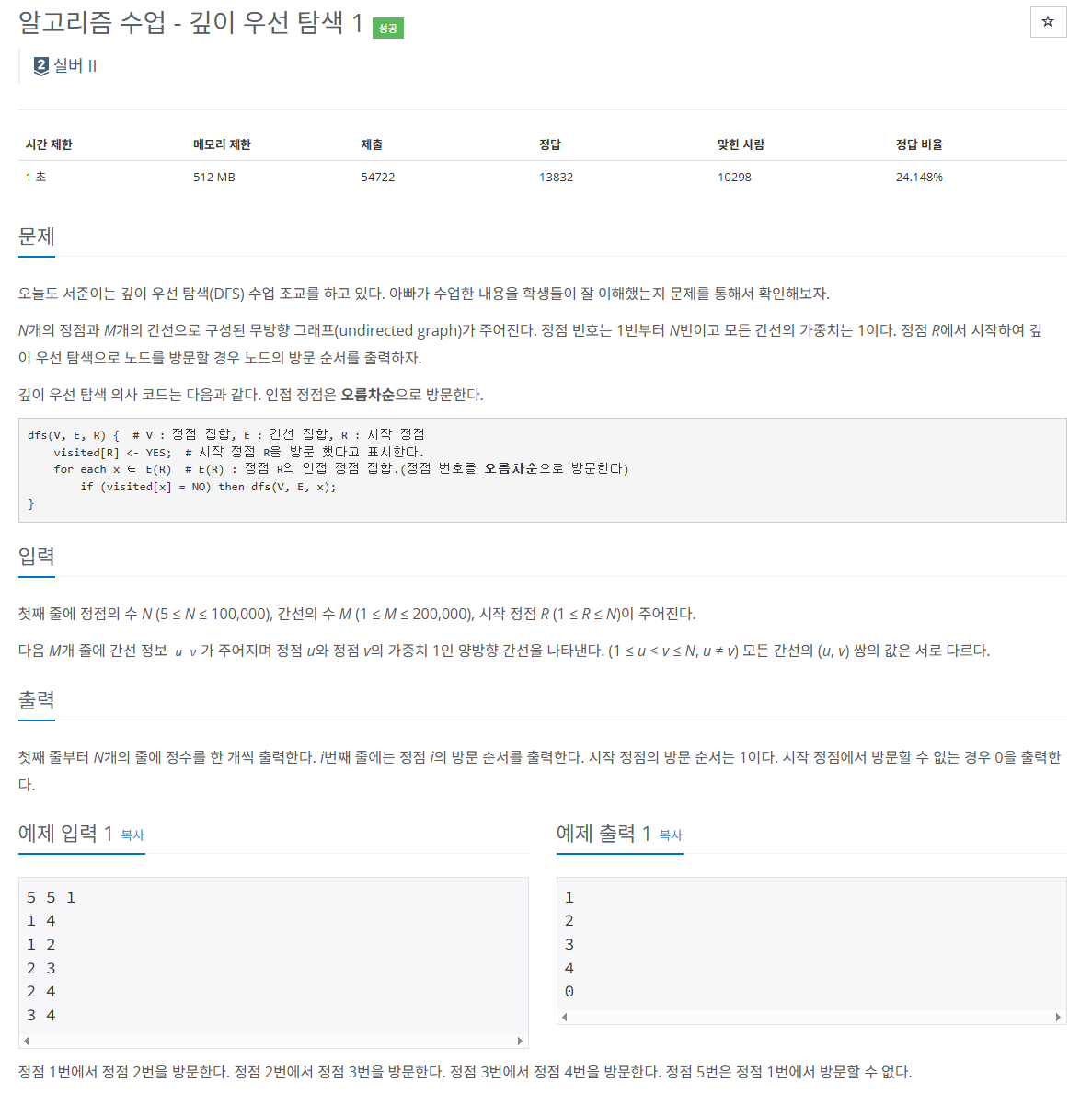
우선 깊이 우선 탐색(dfs)를 처음 풀어보기 때문에 어떤 방식으로 구현이 되어야 하는지 알아보겠다
깊이 우선 탐색(dfs)란
깊이 우선 탐색(DFS, Depth-First Search)은 그래프나 트리에서 한 경로를 따라 최대한 깊이 탐색한 후, 더 이상 갈 곳이 없으면 되돌아와 다른 경로를 탐색하는 알고리즘이다. 이 과정에서 재귀 함수나 스택 자료구조를 사용해 구현할 수 있다.
DFS의 특징
탐색 방식: 한 방향으로 깊이 탐색한 뒤, 막히면 이전 단계로 되돌아가 다른 경로를 탐색한다.
시간 복잡도:
- 인접 리스트: O(V+E) (V는 정점 수, E는 간선 수)
- 인접 행렬: O(V^2)
공간 복잡도: 재귀 호출 스택 또는 명시적인 스택에 의해 O(V) 수준의 메모리를 사용한다.
DFS의 장단점
장점
1. 저장 공간 효율적: 현재 탐색 중인 경로만 저장하면 되므로 메모리 사용량이 적다.
2. 구현 간단: 재귀를 이용해 간결하게 구현할 수 있다.
3. 특정 조건 만족 경로 탐색에 유리: 목표 노드가 깊은 곳에 있는 경우 빠르게 찾을 수 있다.
단점
1. 최단 경로 보장 불가: DFS는 목표 노드에 도달하면 탐색을 종료하기 때문에 최단 경로를 보장하지 않는다.
2. 무한 루프 위험: 순환 그래프에서 방문 여부를 체크하지 않으면 무한 루프에 빠질 수 있다.
3. 비효율성 가능성: 목표 노드와 먼 경로를 먼저 탐색하면 시간이 오래 걸릴 수 있다.
DFS 활용 사례
1. 미로 찾기 및 퍼즐 해결
- 미로에서 한 방향으로 끝까지 이동하며 경로를 탐색하는 데 사용된다.
2. 그래프의 모든 정점 방문
- 그래프의 모든 노드를 방문해야 하는 경우 DFS가 적합하다.
3. 경로 찾기 문제
- 특정 조건을 만족하는 경로를 찾거나, 경로마다 고유한 특성을 기록해야 하는 문제에 활용된다.
4. 강결합 요소(SCC) 찾기
- 그래프에서 강결합 요소를 찾는 알고리즘(예: 코사라주 알고리즘)에서 DFS가 사용된다.
위에서 설명한거처럼 DFS는 보통 재귀를 통해 구현을 한다. 따라서 재귀를 사용하는 방식으로 코드를 짜보았다
구현
using System;
using System.Linq;
using System.Collections.Generic;
using System.Text;
namespace StudyCS
{
class Program
{
static List<List<int>> graph = new List<List<int>>();
static List<int> visitList = new List<int>();
static bool[] visitFlag;
static int cnt = 2;
public static void Main(string[] args)
{
StringBuilder sb = new StringBuilder();
int[] input = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
int n = input[0];
int m = input[1];
int r = input[2];
visitFlag = new bool[n + 1];
// 한 정점이 다른 정점과 연결되어 있는지 확인하는 2차원 List
for(int i = 0; i < n + 1; i++)
{
graph.Add(new List<int>());
}
for (int i = 0; i < m; i++)
{
int[] edge = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
// 1 4로 입력 받았다면 mInfo[1]에 4를 세팅
graph[edge[0]].Add(edge[1]);
// 무방향 그래프일 경우 반대의 경우도 세팅
graph[edge[1]].Add(edge[0]);
}
// 내부 연결된 정점들 정렬
foreach(List<int> edgeList in graph)
{
edgeList.Sort();
}
// 시작 지점 설정
for(int i = 0; i < n + 1; i++)
{
visitList.Add(0);
}
visitList[r] = 1;
visitFlag[r] = true;
Func(r);
// 방문해야하는 정점의 갯수보다 방문한 정점의 갯수가 적은 경우 0을 출력
for(int i = 1; i < n + 1; i++)
{
sb.AppendLine(visitList[i].ToString());
}
Console.WriteLine(sb);
}
public static void Func(int _startPos)
{
for (int i = 0; i < graph[_startPos].Count; i++)
{
int target = graph[_startPos][i];
if (visitFlag[target])
continue;
else
{
visitList[target] = cnt;
cnt++;
visitFlag[target] = true;
Func(target);
}
}
return;
}
}
}
특이점으로는 출력할때의 시간 때문에 stringBuilder를 사용하였다.
아래는 코드에 대한 간략한 설명이다.
인접한 정점에 대한 정보(간선의 정보)를 저장하기 위해 2중 리스트인 graph를 사용하였다.
정점과 간선의 정보가 입력될 때 0이 아닌 1부터 입력이 되기 때문에 n이 아닌 n + 1 크기만큼 설정하였다.
edge에 간선의 정보를 한줄씩 받아 무방향 그래프이므로 반대의 경우까지 graph에 추가하였다
문제에서 요구한 것이 오름차순이므로 정렬을 한 후 빈 리스트를 visitList에 추가하였다.
시작 위치인 r을 1번째로 설정 한 후 방문한 visitFlag를 true로 바꿔주며 재귀를 통해 그래프를 탐색한다.
추가) 이후에 확인해보니 24480 알고리즘 수업 - 깊이 우선 탐색 2는 edgeList.Sort() 이후 edgeList.Reverse()코드만 추가하면 되므로 풀이는 생략함
'BaekJoon' 카테고리의 다른 글
| BFS - 18352 (0) | 2025.09.10 |
|---|---|
| 백트래킹 - 4251 (0) | 2025.09.09 |
| 기하학 - 1002 (0) | 2025.03.29 |
| Greedy Algorithm - 11399 (0) | 2025.03.27 |
| Dynamic Programing - 1463 (0) | 2025.03.26 |